Emotion Recognization App

技术要点

Signal

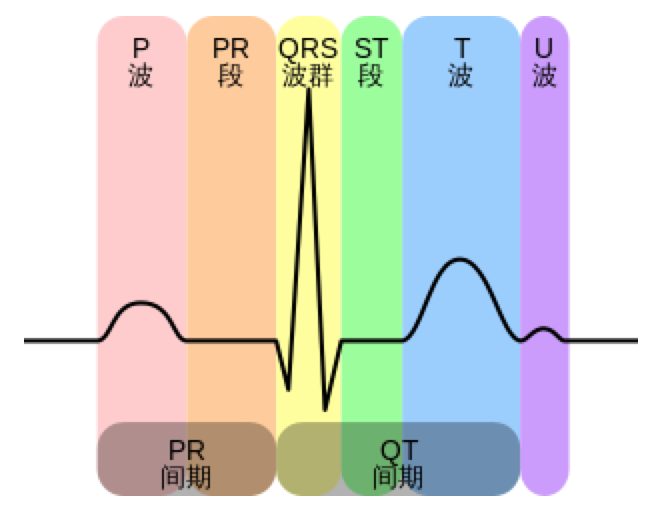
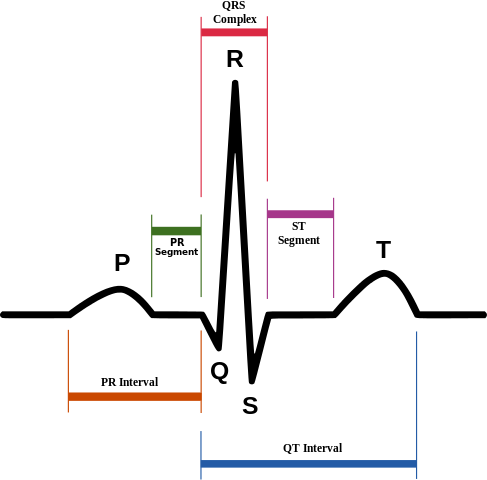
Samples

The sample rate of phone camera is between 5Hz to 30Hz, but the ideal rate is 200Hz. so after geting data from camera, we should use interpolation to do resamples.

Data Preprocess

Denoising

• rpeakdetect

  lowpass = scipy.signal.butter(1, highfreq/(rate/2.0), 'low')
  highpass = scipy.signal.butter(1, lowfreq/(rate/2.0), 'high')
  # TODO: Could use an actual bandpass filter
  ecg_low = scipy.signal.filtfilt(*lowpass, x=ecg)
  ecg_band = scipy.signal.filtfilt(*highpass, x=ecg_low)
  

Smooth

Using Hanning window which length is 500 to make convolution with emotion signal

\[\omega(n)=0.5-0.5cos(\frac{2\pi{n}}{M-1}) \quad 0 \le n \le M-1\]

Normalized

• sklearn.preprocessing.normalize()

QRS Detection

• rpeakdetect

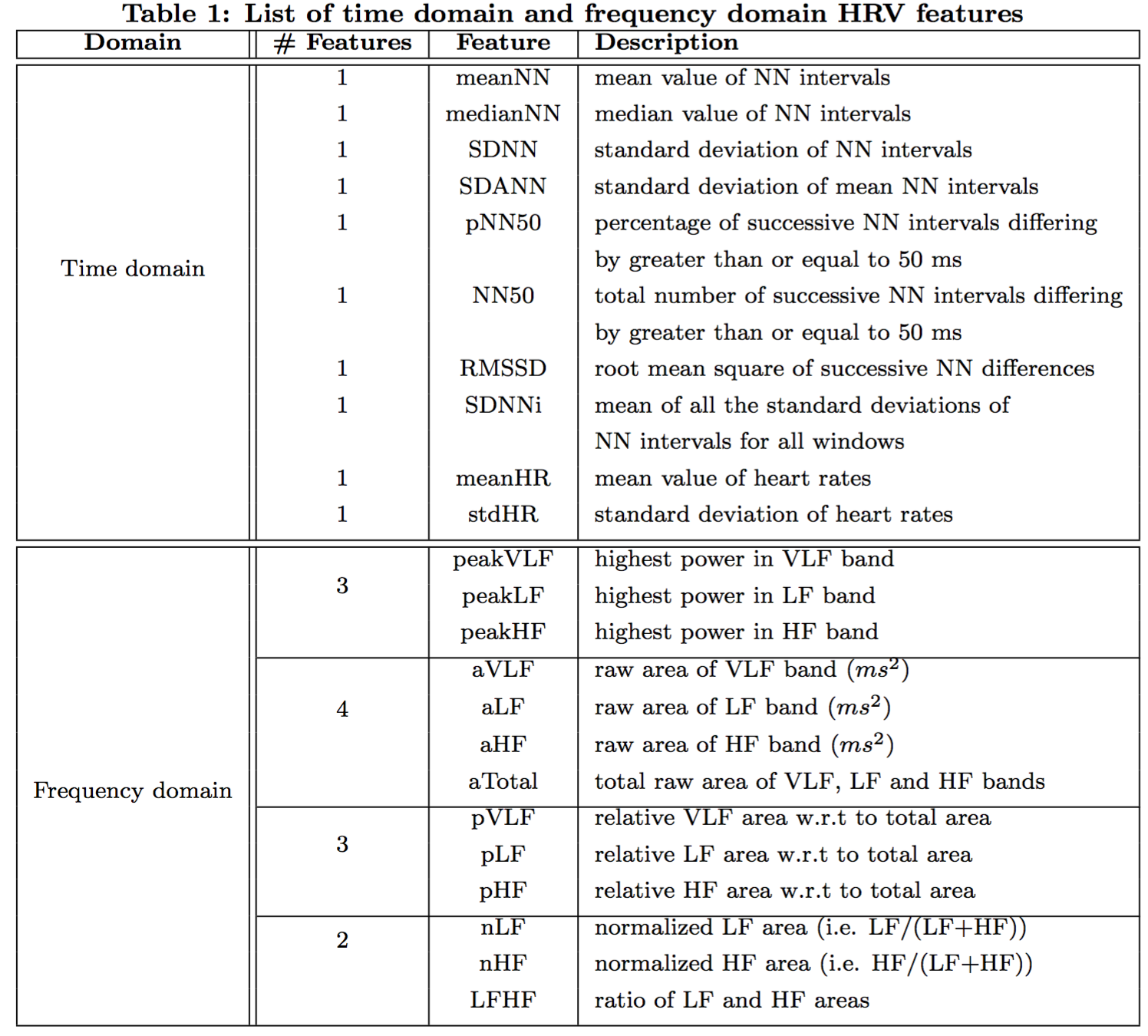
Extract Features

• hrv

Features Defination

• Mean for raw signal

  \[\mu_X=\frac{1}{N}\sideset{}{_{n=1}^N}\sum{X_n}\]

• Mean for normalized signal

  \[\tilde{\mu}_X=\frac{1}{N}\sideset{}{_{n=1}^N}\sum{\tilde{X}_n}\]

• Variance for raw signal

  \[\sigma_X^2=(\frac{1}{N-1}\sideset{}{_{n=1}^N}\sum{( X_n-\mu_X )^2})\]

• Variance for normalized signal

  \[\tilde{\sigma}_X^2=(\frac{1}{N-1}\sideset{}{_{n=1}^N}\sum{( \tilde{X_n}-\tilde{\mu}_X )^2})\]

• First forward difference mean for smoothed signal

  \[\delta_x=\mu(x_{n+1}+x_n)=\frac{1}{N-1}(x_N-x_1)\]

• First forward difference mean for normalized smoothed signal

  \[\tilde{\delta}_x=\frac{1}{N-1}(\tilde{x}_N-\tilde{x}_1)\]

• meanNN

  \[\bar{x}=\frac{1}{N}\sideset{}{_{n=1}^N}\sum{x_n}\]
• medianNN
  • sort \(x_n\) from smallest to biggest
  • if N is odd, \(x_{N/2+1}\) is the median value
  • if N is even, \(\frac{x_{N/2}+x_{N/2+1}}{2}\) is the median value

• SDNN

  \[s=\sqrt{\frac{1}{N}\sideset{}{_{n=1}^N}\sum{(x_n-\bar{x})^2}}\]
• SDANN
  • target arrays is the meanNN of multiple record period
  • calculate the SDNN of target arrays
• pNN50 and NN50 Let’s say:
  • N is the HRV signal length
  • \(N_{50}\) is the number of interval difference of successive NN interval whoes value is greater than or equal to 50ms

  Then: \(pNN50=\frac{N_{50}}{N-1}\ NN50=N_{50}\)

• RMSSD The square root of the mean of the sum of the squares of differences between adjacent NN intervals. \(RMSSD=\sqrt{\frac{1}{N-1}\sideset{}{_{n=2}^N}\sum{(x_n-x_{n-1})^2}}\)

• SDNNi
  • target arrays is the SDNN of multiple record period
  • calculate the mean of target arrays
• meanHR
  • target arrays is the HeartRate of multiple record period
  • calculate the mean of target arrays
• stdHR
  • target arrays is the HeartRate of multiple record period
  • calculate the standard deviation of target arrays

Feature for each signal

• EMG
  • Mean for raw signal Reflect jaw cleaching, frowning and smiling
• GSR
  • Mean for normalized signal
  • First forward difference mean for normalized smoothed signal
• BVP(Blood Volume Pulse) Heart Rate
  • Mean for smoothed signal(no normalized)
  • First forward difference mean for smoothed signal(no normalized)
• Respiration
  • Time domain
    • Mean for normalized signal
    • Variance for normalized signal
  • Frequency domain …
• HRV

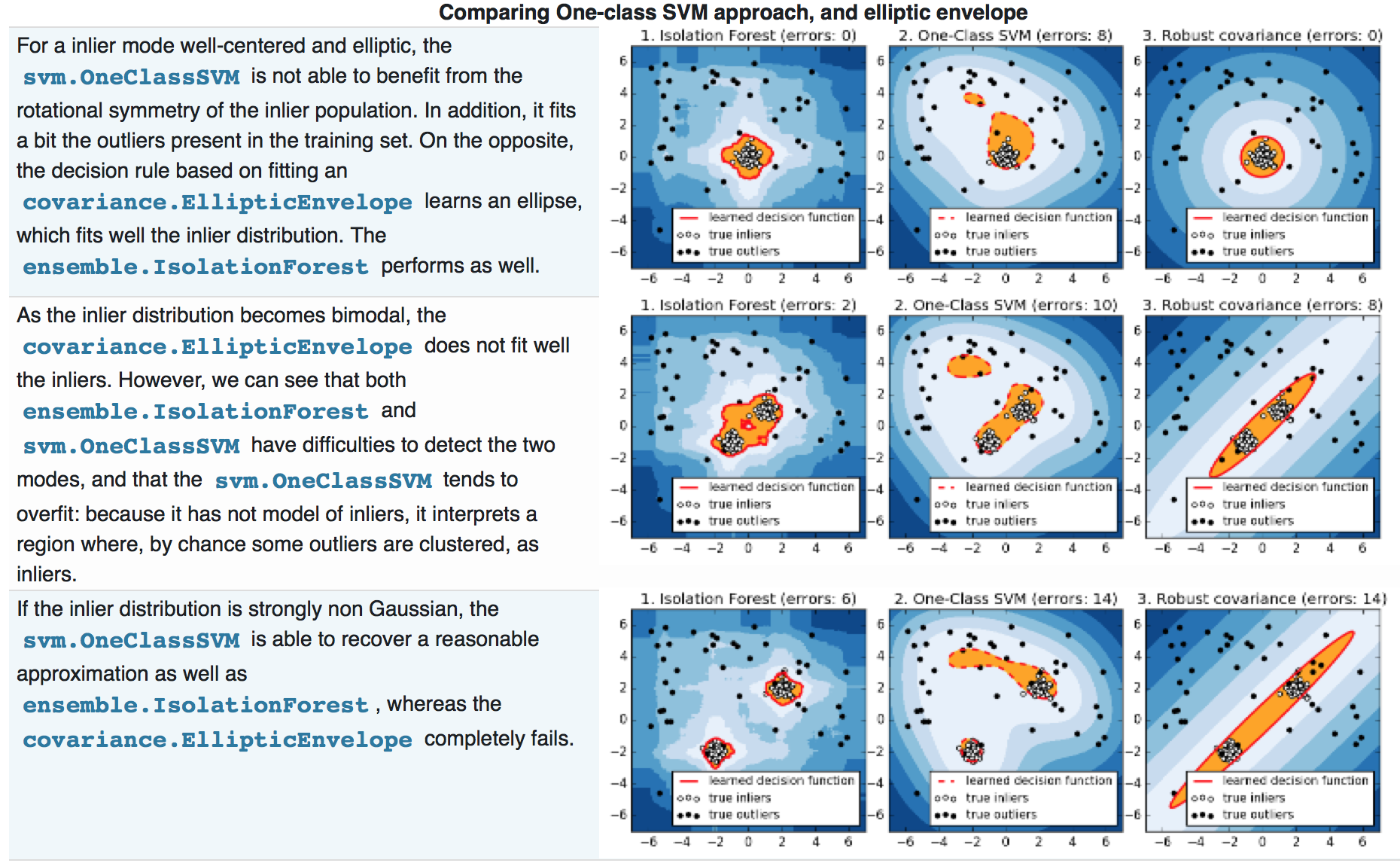
Novelty and Outlier Detection

• One-Class SVM
• Isolation Forest
• EllipticEnvelop

实现思路

• 由于很难找到能够使用的数据集，决定先实现数据处理算法，计算出feature向量，再根据向量间的距离来判断情绪是否有起伏。
• 从目前查到的资料看，使用BVP(Blood Volume Pulse)信号进行情感预测是比较可行的，该信号可通过手机摄像头获取，且有iOS代码库可供参考：HeartBeats
• 剩下需要考虑的问题是该计算哪些feature，以及如何判断情绪起伏，目前能想到的方案是:
  • 按固定时间间隔获取BVP信号
  • 对BVP信号进行预处理并计算feature向量
  • 计算当前时间feature向量与前一次的向量距离，如果距离大于某个阈值则认为情绪发生变化
  • 如果距离小于阈值则将两次向量进行融合，最简单的方法是进行光滑处理 \(X_c=\alpha X_c + (1-\alpha) X_t\)
• 发现一款以HRV为基础的App,HRV4Trainning, 对HRV的各个features分析的很透彻，允许用户记录HRV并加注标签，和我以前的想法很类似。不过它是一款收费软件，目前用户10000，由意大利开发，主要针对体育锻炼。这个软件从侧面证明了我以PPG为信号输入，HRV为信号源的想法是没错的。
• 发现如果要判断情绪变化，只需判断当前feature是否异常就可以了，这就用到了无监督学习算法，目前看到的有One-Class SVM, Isolation Forest, EllipticEnvelop, 从查到的资料 看Isolation Forest 对高维度变量的准确度最高，暂时选用这个算法进行分析。

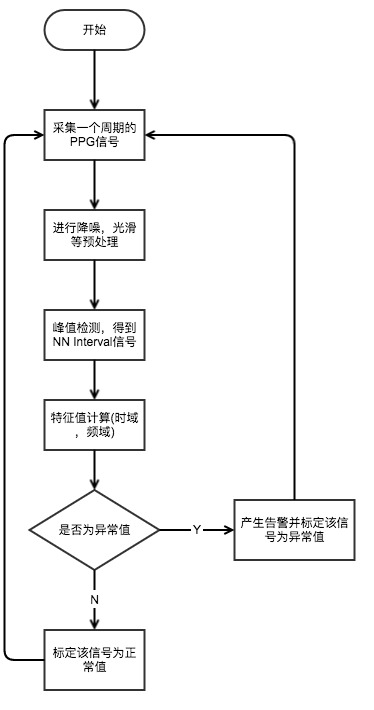
算法流程